Расширение цилиндров и конусов основано на методе расширения граненой поверхности, описанном выше. В общем случае цилиндрические поверхности аппроксимируются пирамидальными поверхностями, конусы аппроксимируются пирамидами, а затем строится приблизительная развертка поверхности.
Свойства развёрток
Развертка поверхности F — это плоская фигура, получающаяся в результате совпадения плоскости F и плоскости Σ (рис. 5.1). В картинной геометрии Σ-плоскость является одной из плоскостей проекций.
Поверхностная прокатка широко используется в машиностроении, так как многие технические конструкции изготавливаются из листов. Части таких конструкций, представляющие собой сверла, используются при изготовлении тонкостенных контейнеров, воздуходувок, промышленной вентиляции и воздушного транспорта, формованных деталей пылеуловителей, деталей подъемно-транспортного оборудования и т.д. (рис. 5.2).
Подготовка поверхности

Бурение.
Поверхности F, которые можно совместить с плоскостью Σ без зазоров и складок, могут быть открыты. К ним относятся все многогранники (см. 4.1), цилиндрические и конические поверхности (см. 3.2.1.3, рис. 3.55 b-c) и буфы (см. 3.2.1.3, рис. 3.57). Все остальные поверхности не развиваются в плоские, поэтому если они состоят из листов, то приближаются развитые поверхности (призмы, пирамиды, цилиндры, конусы). В этих случаях используются так называемые обычные буры (см. пункты 5.4.1.3 — 5.4.1.4).
Основные характеристики перфорации следующие
(a) Линия l на поверхности F соответствует линии на разработке
(b) Параллельные линии на поверхности F соответствуют параллельным линиям на транце
c) длина (натуральная величина) любой линии s на поверхности P равна длине линии на расширении
d) угол α между линиями r и s на поверхности P равен углу между этими линиями при разворачивании
(e) площадь s профиля на поверхности F равна плоскости соответствующего профиля при разворачивании
(f) Если линия в профиле соответствует кривой s на поверхности F, то кривая s является геодезической линией на поверхности F. Длина геодезической дуги MN — наименьшая из всех возможных дуг MN на поверхности F.
Описанные свойства интерпретируются геометрически на рис. 5.3.
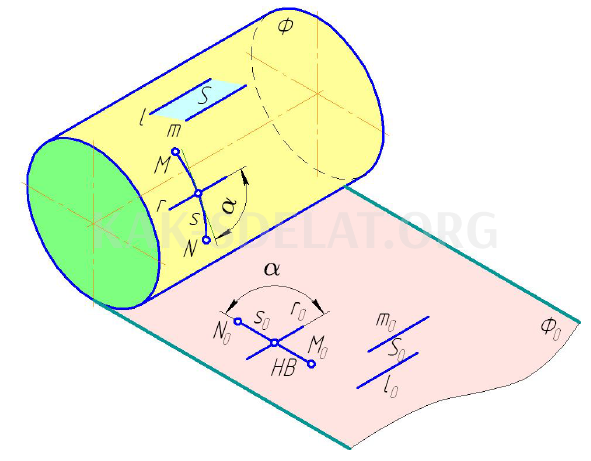
Свойства строчной развертки
Геодезическая линия (от греч. geodesy — деление земли) — это линия минимальной длины, проходящая через две точки на поверхности. Эта линия является прямой линией поверхностного трения.
Геодезические широко используются в неевклидовой геометрии, в теоретических и практических задачах геодезии, а также в науках, изучающих измерение пространства, включая размер и форму Земли и ее гравитационного поля.
Развёртывание поверхности многогранника
Многогранник — это форма, получаемая в результате последовательного выравнивания граней и плоскостей многогранника. Разворачивание всегда происходит внешней стороной (лицом) к наблюдателю.
Метод физического лица
Согласно свойству разворачивания (см. раздел 5.1), каждая грань многогранника F сохраняет свою длину при разворачивании. Для определения этого используются методы начертательной геометрии.
На рисунке 5.4 показаны горизонтальная и фронтальная проекции треугольной пирамиды САБК. На рисунке 5.4 показаны горизонтальная и фронтальная проекции треугольной пирамиды САБК. Основание ABC показано на P1 натуральной величины A1B1C1, так как оно находится на горизонтальном уровне. Для определения натуральных величин SAB, SBC и SCA используйте метод вращения вокруг горизонтальной проекционной оси I, проходящей через верхнюю S пирамиды. отрезки — это натуральные значения SA, SB, SB и SC пирамиды. На этих гранях строится расширение пирамиды. Вырезав плоский участок из контура расширения и соединив одноименные реберные кости путем складывания по линиям сгиба, можно взять поверхность конкретной пирамиды SABC.
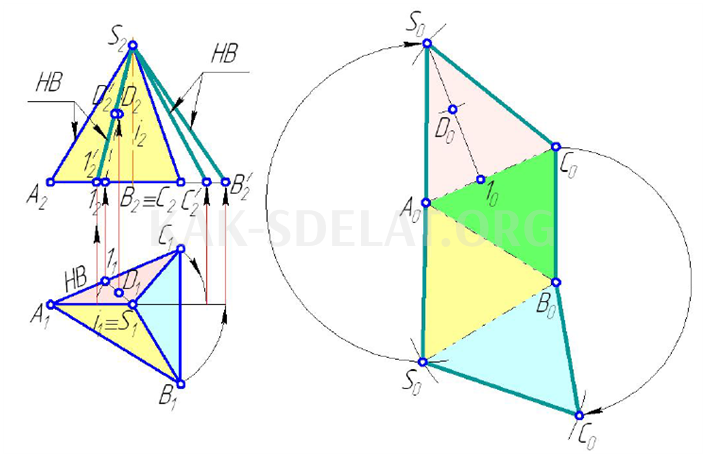
Метод естественного человека
Применяется метод вспомогательного раздела, устанавливая любую точку d пирамиды на расширение. Точка d принадлежит грани S ABC. Через S и точку D проектируется участок S-1, точка 1 которого относится к основанию ABC пирамиды. Определяется натуральная величина участка S-1, длина которого равна длине выступа стандартного участка колеса, часть которого определяется как равная длине выступа.
Обычный метод разреза
Метод обычного разреза используется для конструирования призматических складок с прямыми краями.
Содержание метода нормальных сечений
Призмы пересекаются в любой точке на уровне S перпендикулярно их граням. Ряды 1-2- … нормального пересечения … определяются физическими величинами призмы. Эта линия является многоугольным уровнем с числом сторон, равным числу сторон призмы. Прямые 1-2- … расширяется, образуя прямую … Вертикальная диаграмма, вписанная по обе стороны от точки …. Уровень резки S
На рисунке 5.5 показаны две проекции треугольной призмы ABCDEF с использованием горизонтальных ребер AD, BE и CF. Уровни реза были вставлены перпендикулярно граням призмы (горизонтальный след S1 перпендикулярен горизонтальной проекции граней призмы). Уровень S пересекает призму треугольниками 1-2-3, точки которых принадлежат ребрам AD, BE и CF соответственно. Замена уровня проекции определяет натуральное значение нормального сечения пересечения (ось параллельна S1). Затем треугольник развивается в виде прямого отрезка, длина которого равна соответствующей стороне треугольника. Перпендикуляры, проведенные по обе стороны от точки, используются для построения отрезка, равного по длине проекции.
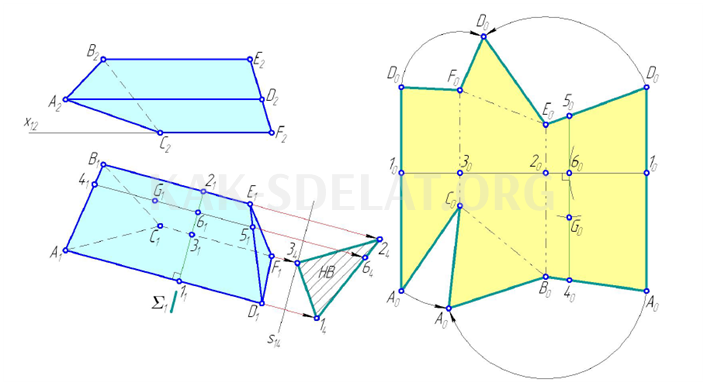
Нормальный метод пересекающихся отрезков
Чтобы установить любую точку g призмы во взрывном виде, используйте метод сечения дюбеля. Точка g принадлежит анодефолду. Проведите отрезки 4-5 через точку g параллельно грани призмы. Участок AB относится к точке 4, а участок DE — к точке 5. Найдите точку 6 участка 4-5 на С. Точка 6 относится к участку 1-2. Разделите дисплей на части. Его часть равна проективной длине от точки разделенной призмы.
Метод складывания
Для разворачивания призмы используется метод элюминирования. Его основание параллельно уровню проекции, а боковые грани параллельны проекции другого уровня.
Пункты 1, 2, … От основ … Основание верхней поверхности призмы начинается перпендикулярно боковой … Эти лучи предназначены … Длина секции составляет … Естественная цена раздела, ….
На рисунке 5.6 показаны две проекции треугольной призмы на основе горизонтального уровня и фронтального обода после 1-2-3. Фронтальная проекция проектирует лучи, перпендикулярные фронтальным проекциям этих лучей. Точки располагаются последовательно так, чтобы длина частей равнялась натуральной величине отрезка.
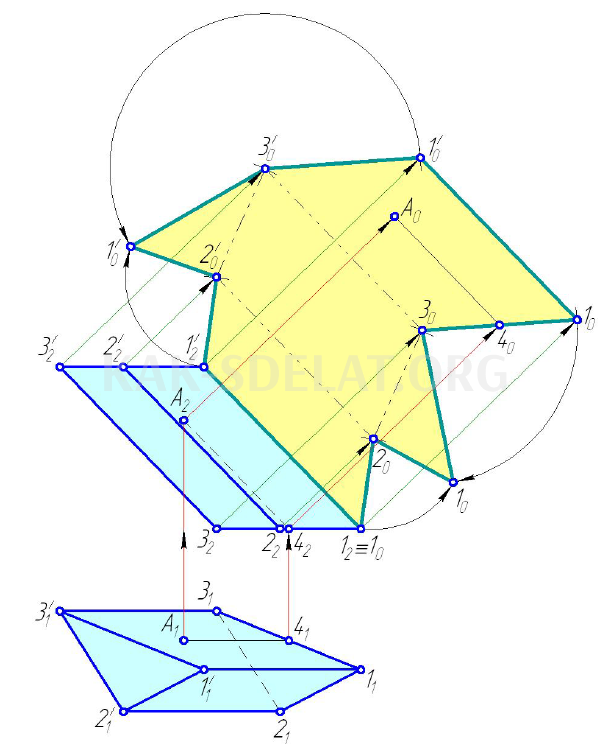
Метод расширен
Метод вспомогательных лучей применяется для определения любой точки A призмы разворачивания. Через точку А проводится отрезок, параллельный грани призмы. В точке 4 этот отрезок принадлежит отрезкам 1-3 основания. Проекция производится лучами, перпендикулярными фронтальной проекции грани призмы. Из точки, принадлежащей отрезку обрезки, строится отрезок, параллельный отрезку, до пересечения с проекцией.
Развёртывание поверхностей тел вращения
Что касается поверхностей, то они делятся на две категории. Они развертываются и могут быть выровнены с уровнями без разрывов и складок, и не могут быть выровнены с уровнями без разрывов и складок. Все многогранные поверхности являются только линейчатыми и могут быть развиты между линейчатыми формами, соседние образования которых пересекаются либо параллельно (цилиндрические), либо в некоторой точке (конические).
Из всего многообразия поверхностей вращения точное вращение имеют только прямые цилиндры и конусы (рис. 5.7-5.8).
Поверхность прямого кругового цилиндра развивается в прямоугольной форме, одна сторона которой равна длине нормального разреза (диаметр окружности d), а другая равна высоте цилиндра h (рис. 5.7). При необходимости цилиндр дополняется диаметральной окружностью d, верхним основанием и верхним основанием. Метод построения прямой используется для определения точки A прямого цилиндра. Определяется угол A и проектируется производственная линия. Он располагается на расстоянии. Высота точки равна высоте точки A.
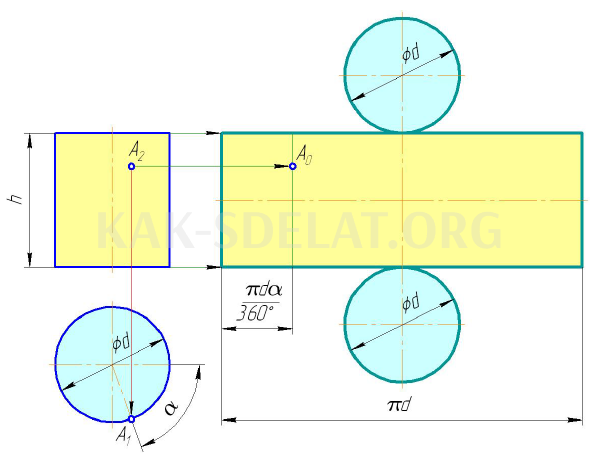
Цилиндрическое обнаружение
Поверхность прямого конуса простирается до круговой области с центром на вершине S конуса. Радиус области равен длине l линии, образующей конус — угол φ = 180° — d/L, где d — диаметр основания конуса (рисунок 5.8). При необходимости контур конуса дополняется циклом диаметра d. Метод построения прямых используется для определения точки A прямого конуса. Угол A определен, производственная линия спроектирована по проекту, и ее положение определяется углом b = 0,5AD/L. Эта точка находится на расстоянии, равном естественному размеру SA.
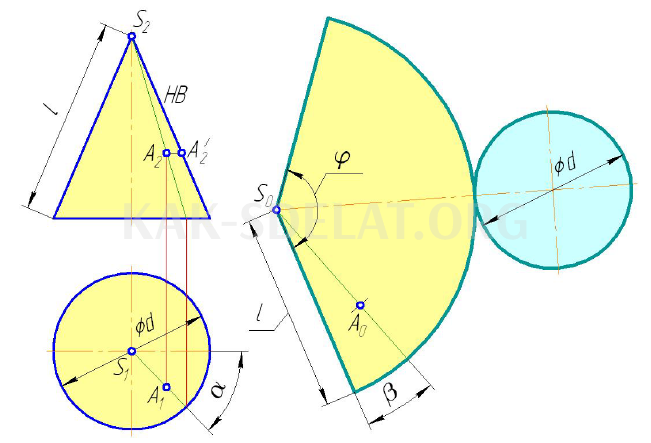
Чертежные конусы.
Приближённое и условное развёртывание кривых поверхностей
Приближение от одной поверхности к другой (лат. по момераре) используется для получения приблизительного условного скана. Подход заключается в замене поверхности на приближенную поверхность. Он использует определенные характеристики (форма, площадь, кривизна) для приближения к заданной поверхности или имеет такую степень точности.
Методы приближения к поверхности
Подход к развитой поверхности (за исключением прямых круговых конусов и цилиндров) состоит из захода. Это связано с тем, что криволинейные поверхности при расширении приближаются к зарегистрированным многогранным поверхностям (рисунок 5.9).
Методы призматических поверхностей
Например, цилиндрическую поверхность условно заменяют призмой (рис. 5.9 а), коническую поверхность пирамидой (рис. 5.9 б).
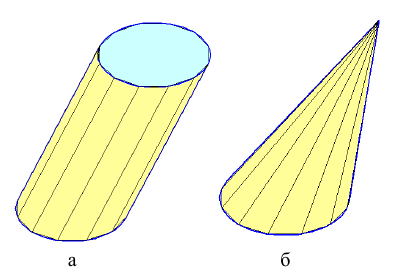
— Мы подходим к телу революции со стороны многогранника.
Методы призматических поверхностей используются для построения приближенных планов цилиндрических поверхностей
Методы для призматических поверхностей
Цилиндрическая поверхность записывает призму. Количество его сторон напрямую влияет на точность проектирования профиля цилиндра. Призма разрабатывается обычным методом поперечного сечения или прокатки (см. разделы 5.2.2-5.2.3). В знаки призмы вписаны плавные кривые, которые являются приблизительными контурами валика цилиндра. При необходимости контуры цилиндра дополняются нижним и верхним основаниями.
На рисунке 5.10 показана сложная конструкция эллиптического цилиндра, к поверхности которого подходят 12 призм. Последняя конструкция изготавливается методом прокатки. Плавные кривые (Sine) проектируются через точки и образуют контур разворачивающихся роликов. Скульптурирование завершается в нижнем и верхнем слоях цилиндра.
Метод пирамидальной поверхности
Для оформления боковых сторон конуса используется метод пирамидальной поверхности.
Метод пирамидальной поверхности
Нарисуйте пирамиду на поверхности конуса. Примерная конструкция этой пирамиды создана методом естественного фасада (см. пункт 5.2.1). Плавные кривые, которые являются угольными контурами конуса, проектируются через точки пирамиды. При необходимости контур конуса дополняется у его основания.
Аппроксимация — это научный метод замены объекта другим, более простым объектом, который приближается к оригиналу.
Необходимо различать такие понятия, как подход и условное складывание. Приближающееся разворачивание относится к поверхности, которая была развернута. Для развернутых поверхностей строится условное складывание.
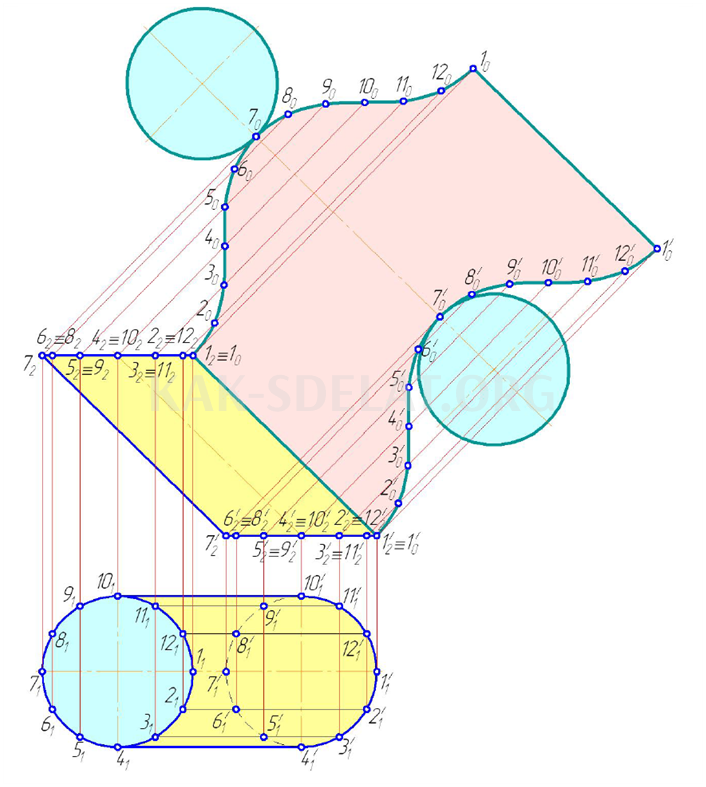
Эллиптические ролики должны быть развернуты.
Форма. 5.11 показана сложная конструкция эллиптического конуса, к поверхности которого подходит 12-гранная пирамида. Последняя конструкция изготавливается по методу Natural Face Method. Через точки, образующие контур конуса, вырезаны плавные кривые. Разработка завершается у основания конуса.
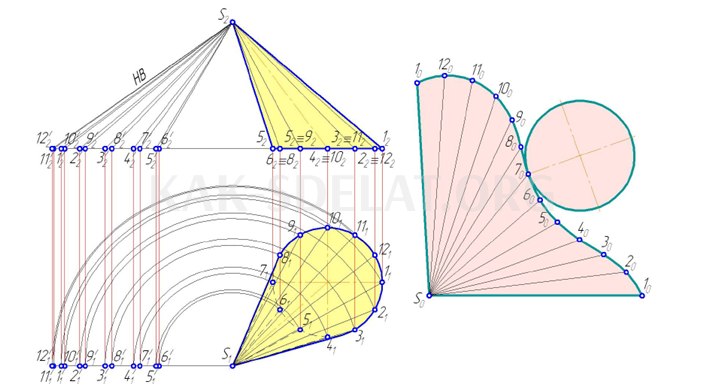
Эллиптический конус
Цилиндрическая поверхность
Для нерастущих поверхностей. Производятся зависимости, включая нелинейные поверхности. Основными методами конструирования кондиционной мебели являются.
(a) метод цилиндрических поверхностей, метод
(b) метод конической поверхности, и
(c) треугольный метод.
Методы цилиндрических поверхностей
Криволинейные поверхности описываются серией цилиндрических поверхностей, соединенных точками и линиями. Результирующее расслоение является условным термином на поверхности кривой поверхности.
Рисунок 5.12. Строятся условные термины на сфере. Вокруг поверхности описаны шесть одинаковых цилиндрических поверхностей. Одна из этих поверхностей имеет фигурные линии. Длина этих линий фигуры равна длине горизонтальной проекции. Расстояния между линиями формы одинаковы, т.е. длина дуги SA, т.е. одна из шести цилиндрических поверхностей переднего выступа имеет форму лепестка, проходящего через концы линий формы, равные между собой на расстоянии, равном длине дуги. Добавляются еще пять, чтобы построить воображаемое развитие сферы.
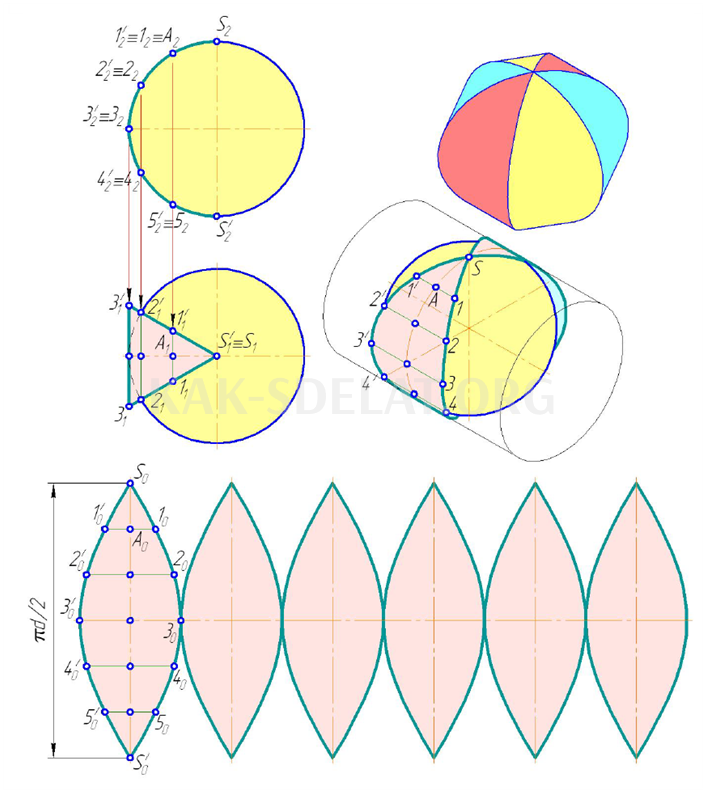
Складывание сфер Условное.
На рисунке 5.13 показана схема открытого тора. Вокруг его поверхности нарисованы двенадцать одинаковых цилиндрических поверхностей. На одной из этих поверхностей есть линии, образующие прямую линию. Длина этих линий равна длине фронтальной проекции. Расстояние между линиями одинаково и равно длине дуги SA, то есть длине горизонтальной проекции S1A1. . Одна из 12 цилиндрических поверхностей представляет собой фигуру, контур которой проходит через концы линий, равноотстоящих друг от друга на одинаковом расстоянии, равном длине дуги S1A1. Прибавляя к полученной части еще 11, строится условное расширение кольца.
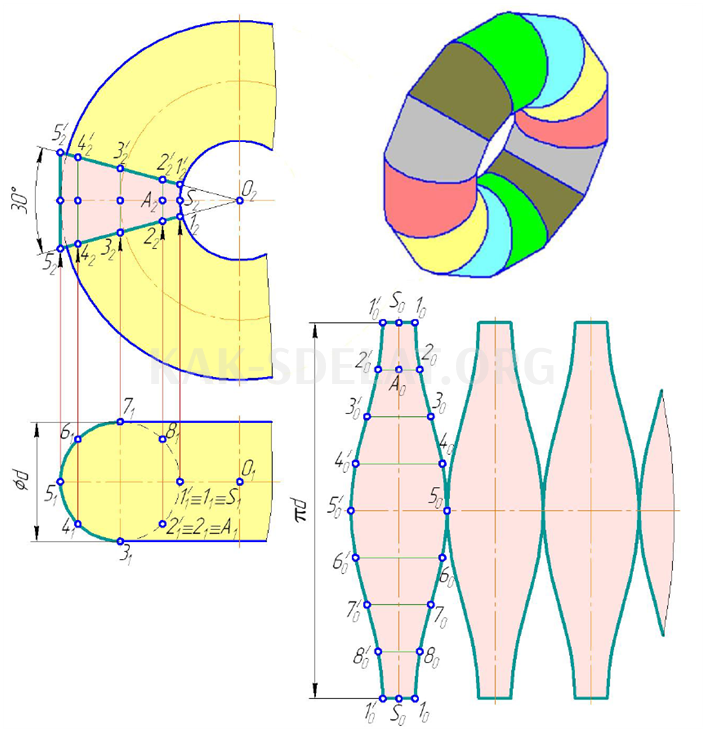
Условное расширение открытого тора
Метод конической поверхности
Метод конических поверхностей используется для условного расширения замкнутых тел вращения (например, эллипсоидов, парабол, эллипсоидов, гиперболических поверхностей, замкнутых торов).
Сущность метода конических поверхностей
Сегмент поверхности описывается набором конических кривых, которые складываются и выравниваются с помощью точек и линий. Результирующая фреза представляет собой условную фрезу кривых поверхностей.
На рисунке 5.14 показано условное расширение сферы. Цилиндрическая поверхность с различными вершинами и шесть конических поверхностей описаны вокруг ее поверхности. Длины составляющих линий одинаковы и равны длине проекции. Угол и радиус конусов определяются, как описано в разделе 5.3.
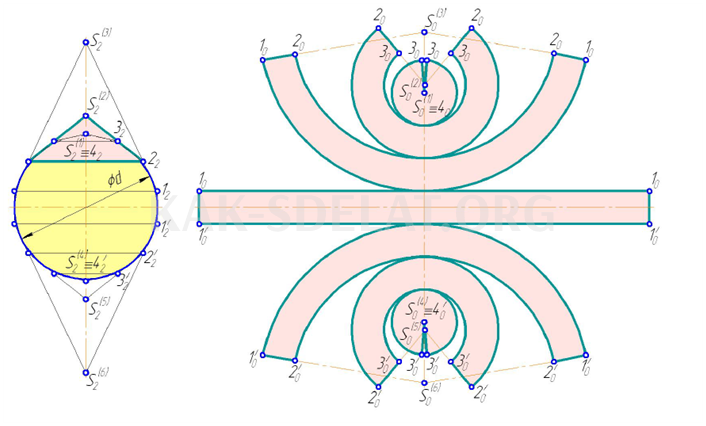
Условное расширение сферы
На рисунке 5.15 показано условное расширение эллипсоида. Цилиндрическая поверхность с различными вершинами и шесть конических поверхностей описаны вокруг поверхности Длина образующих линий может быть различной и определяется их фронтальными проекциями. Угол и радиус конусов определяются, как показано в разделе 5.3.
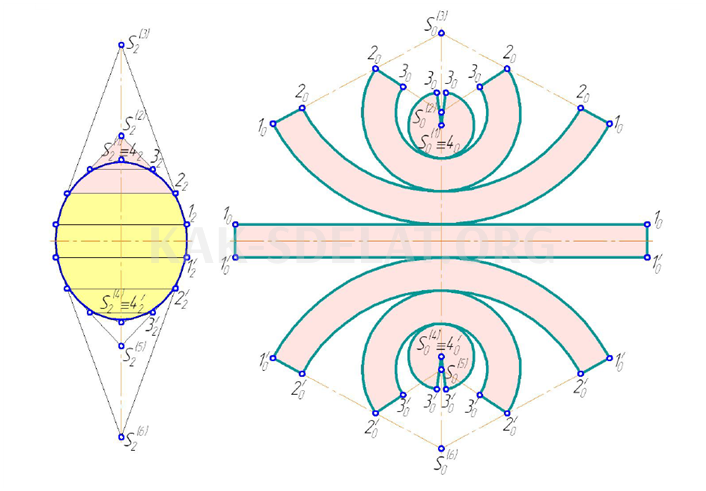
Условное расширение эллипсоидов
Методы триангуляции
Методы триангуляции используются для разворачивания многогранников, приближенного разворачивания цилиндрических и конических поверхностей и поверхностей с поворотом краев (бутов), а также условного разворачивания развернутых поверхностей.
Методы триангуляции
Поверхности делятся на треугольники с общими краями. Физические величины этих треугольников объединяются с помощью общих ребер. Внешний контур полученной плоской фигуры является аппроксимацией или условной складкой данной поверхности.
Форма. 5.16 — примерное развитие загрузки F. Последняя разделена множеством треугольников с вершинами 1, 2, …. и разделена множеством треугольников с обратными ребрами и принадлежащих одной из линий l поверхности F. Стороны 1-2, 2-3, … треугольников определяются вращением вокруг оси проекции. Треугольники 1-2-3, 2-3-4, …, объединенные общим ребром Физические величины создаются с помощью найденных сегментов. Полученный контур плоскости является примерным развитием F-образного ствола.
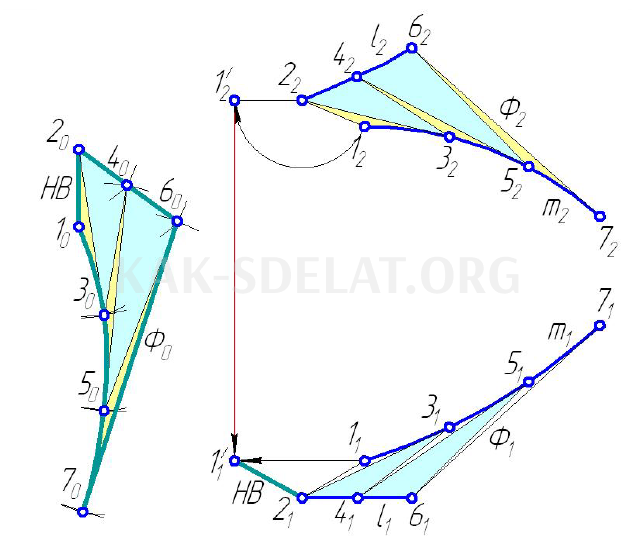
Примерное развитие ботинка
На рисунке 5.17 показан подход к поверхности произвольного космического тела. На рисунке 5.17 показано примерное расположение поверхностей любого пространственного тела. Его поверхностями являются точки 1, 2, …, которые относятся к верхней и нижней частям тела соответственно. A, B, … Тело разделено на треугольники, стороны которых спроектированы под . Натуральные значения сторон треугольника определяются вращением вокруг горизонтальной оси, проходящей через точки b, c. Натуральная цена треугольника получается с помощью найденных отрезков, и треугольник совмещается с общими сторонами. Получившийся контур плоской формы приблизительно разворачивает поверхность тела.
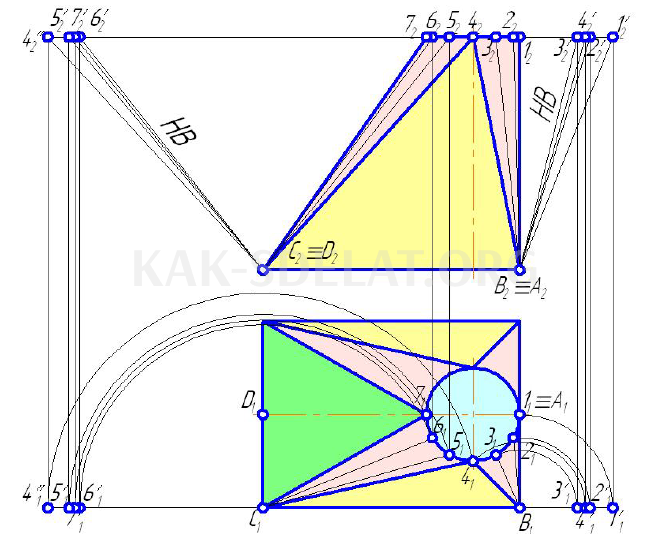
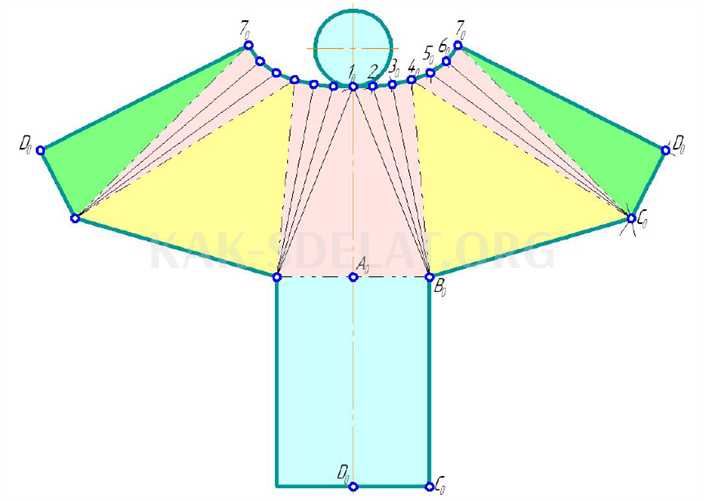
Треугольная поверхность отбрасывается
Примеры и образцы решений:.
Услуги по проектированию:.
Отправляйте задания днем и ночью.
Официальный сайт Brilijono Banataria Валерий Эвант Екатеринбургский государственный научно-исследовательский институт им. проф.
Все права интеллектуальной собственности на загруженный материал сохраняются за бенефициарами этого материала. Коммерческое и/или иное использование запрещено за пределами материалов предварительного изучения NataliblileNova.ru. Публикация и распространение опубликованных материалов не предназначены для получения коммерческой и/или иной выгоды.
Этот сайт предназначен для облегчения образовательного пути студентов. Наталья Брилёнова не предлагает и не оказывает товары и услуги.
При копировании материалов ссылка на сайт Natalibrilenova.ru обязательна.


















